Herons formel
Herons formel anger sambandet mellan en godtycklig triangels area och dess sidor a, b, c samt semiperimetern (halva omkretsen) s enligt[1]
där alltså
Formelns namn kommer från den grekiske matematikern Heron, men formeln upptäcktes troligen inte av honom, utan av Arkimedes.[2]
Herons formel för trianglar är ett specialfall av en mer generell identitet för cykliska fyrhörningar. Genom att nyttja Herons formel och den aritmetiska-geometriska olikheten kan man bevisa den isoperimetriska egenskapen för liksidiga trianglar.
Bevis
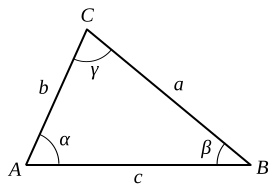
redigeraLåt vara sidorna i en triangel och låt vara motstående vinkel till sidan . Enligt cosinussatsen gäller
Detta ger (via trigonometriska ettan):
Triangelns höjd mot basen har längden varav följer (med hjälp av konjugatregeln och kvadreringsreglerna):
Se även
redigeraReferenser
redigera- ^ Kendig, Keith (2000). ”Is a 2000-year-old formula still keeping some secrets?”. The American Mathematical Monthly 107 (5): sid. 402–415. doi:. https://www.maa.org/programs/maa-awards/writing-awards/is-a-2000-year-old-formula-still-keeping-some-secrets. Arkiverad 29 maj 2024 hämtat från the Wayback Machine.
- ^ ”Fórmula de Herón para calcular el área de cualquier triángulo” (på spanska). Spanien: Ministerio de Educación, Cultura y Deporte. 5 januari 2004. http://recursostic.educacion.es/descartes/web/materiales_didacticos/formula_heron/formula_de_Heron.htm. Läst 29 oktober 2022.

