Cosinussatsen

Cosinussatsen relaterar längden av en sida i en godtycklig triangel till längderna av de andra två samt den till sidan motstående vinkeln.

Antag en triangel med sidlängderna a, b och c och med vinklarna α, β och γ:

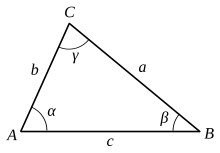
Då gäller att

$a^{2}=b^{2}+c^{2}-2bc\cdot \cos \alpha$

$b^{2}=a^{2}+c^{2}-2ac\cdot \cos \beta$

$c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma$

Om någon vinkel är rät erhålls Pythagoras sats då cosinus för en rät vinkel är 0.

Bevis

Bevis med Pythagoras sats

Eftersom vinkeln mellan $h$ och $c$ är rät, ger Pythagoras sats:

$\ a^{2}=\left(a\cos \beta \right)^{2}+h^{2}$ och $b^{2}=\left(b\cos \alpha \right)^{2}+h^{2}\Leftrightarrow h^{2}=b^{2}-\left(b\cos \alpha \right)^{2}$

vilka ger:

$\ a^{2}=\left(a\cos \beta \right)^{2}+h^{2}=\left(a\cos \beta \right)^{2}+\left(b^{2}-\left(b\cos \alpha \right)^{2}\right)$

Enligt definitionen på cosinus är:

$|{\overline {BD}}|=a\cos \beta$ och $|{\overline {DA}}|=b\cos \alpha$

och då $c=|{\overline {BA}}|=|{\overline {BD}}|+|{\overline {DA}}|=a\cos \beta +b\cos \alpha$ får vi:

$\ a\cos \beta =c-b\cos \alpha$

vilket om det insätts i uttrycket för $\ a^{2}$ ger

$a^{2}=\left(c-b\cos \alpha \right)^{2}+b^{2}-\left(b\cos \alpha \right)^{2}=c^{2}-2bc\cdot \cos \alpha +\left(b\cos \alpha \right)^{2}+b^{2}-\left(b\cos \alpha \right)^{2}\Rightarrow$

$a^{2}=b^{2}+c^{2}-2bc\cdot \cos \alpha$

Bevis med avståndsformeln

En triangel har sidorna a, b, c. Genom att placera triangeln i ett koordinatsystem kan sidlängderna beräknas enligt avståndsformeln med

$A=(b\cos \theta ,b\sin \theta ),\quad B=(a,0),\quad C=(0,0)$

Med hjälp av avståndsformeln kan längden av sidan c skrivas som

$c={\sqrt {(a-b\cos \theta )^{2}+(0-b\sin \theta )^{2}}}\quad \Rightarrow$

$c^{2}=(a-b\cos \theta )^{2}+(-b\sin \theta )^{2}$

$c^{2}=a^{2}-2ab\cos \theta +(b\cos \theta )^{2}+(b\sin \theta )^{2}$

$c^{2}=a^{2}+b^{2}(\sin ^{2}\theta +\cos ^{2}\theta )-2ab\cos \theta$

och slutligen (via "trigonometriska ettan": $\sin ^{2}\theta +\cos ^{2}\theta =1$)

$c^{2}=a^{2}+b^{2}-2ab\cdot \cos \theta$

Se även

• Areasatsen
• Sinussatsen
• Tangenssatsen
• Sinus
• Cosinus
• Tangens