Vinkelhastighet

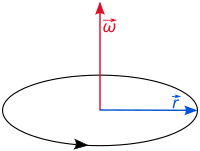
Vinkelhastighet (rotationshastighet, eller vinkelfrekvens) är mått på ett föremåls rotation per tidsenhet kring sitt rotationscentrum. SI-enhet för vinkelhastighet är radianer per sekund. Ofta används den grekiska bokstaven ω för att beteckna vinkelhastighet mätt i denna enhet. Om en punkt på ett roterande föremål har avståndet r till rotationsaxeln och rör sig med hastigheten v, kan rotationshastigheten beräknas till v/r radianer per sekund.

Vinkelhastighet
Grundläggande
Alternativnamn	Rotationshastighet
Definition	Rotation per tidsenhet kring sitt rotationscentrum
Storhetssymbol(er)	${\vec {\omega }}$
Enheter
SI-enhet	rad·s−1
SI-dimension	T−1

Samband

Multipliceras vinkelhastigheten med den tid rotationen pågått, ω•t, fås den vinkel mätt i radianer som uppnåtts vid denna tid.

Ett varv är 2π radianer och relationen mellan vinkelhastigheten ω och frekvensen f är

$\omega =2\pi f\,$

Exempel: Frekvensen f = 5 Hz motsvarar vinkelhastigheten ω = 2π rad • 5 Hz ≈ 31,4 rad/s. Efter 10 sekunder har föremålet roterat ω•t ≈ 31,4 rad/s • 10s = 314 rad.

Accelerationen är v²/r, riktad mot centrum

En punkts hastighet v är direkt proportionell mot vinkelhastigheten ω och avståndet r till rotationsaxeln. Detta gäller inte för förmål som rullar med glid:

$v=\omega r=2\pi rf.\,$

${\vec {v}}={\vec {\omega }}\times {\vec {r}}$

När vinkelhastigheten är konstant, talar man om likformig cirkulär rörelse. En punkt färdas då med konstant hastighet längs en cirkelbana, men dess riktning ändras kontinuerligt och punkten har en acceleration riktad mot cirkelns centrum. Figuren till höger visar att dess storlek är proportionell mot hastigheten och mot vinkelns ändringshastighet dβ/dt. Centripetalaccelerationen ges därför av

$a={\frac {{\rm {d}}v}{{\rm {d}}t}}=v{\frac {{\rm {d}}\beta }{{\rm {d}}t}}=v\ \omega =\omega ^{2}r={\frac {v^{2}}{r}}$

Denna centripetalacceleration skall ej förväxlas med vinkelaccelerationen, som ger ändringen av vinkelhastigheten per tidsenhet,

$\alpha ={\frac {{\rm {d}}\omega }{{\rm {d}}t}}$

Tillämpningar

Vinkelhastigheten (röd) som pseudovektor. Då rotationen är moturs är vektorn enligt konvention (vilket är orsaken till att den är en pseudovektor) riktad uppåt

Exempel på rotationshastigheter inom klassisk mekanik:

• En satellit eller en planet som roterar i en cirkulär bana kring sitt rotationscentrum. Satelliten rör sig då med konstant rotationshastighet.
• En kropp roterar kring en fix axel utan påverkan av yttre krafter. Varje punkt roterar då med konstant rotationshastighet relativt axeln.
• Om rotationsaxeln inte är fix, kan rörelserna bli komplicerade, med precession och nutation av rotationsaxeln. För ett fritt föremål går rotationsaxlarna alltid genom kroppens tyngdpunkt. Rörelseekvationerna är lösbara om föremålet är en stel kropp.

Rotationshastigheten är en pseudovektor.

Externa länkar

• Wikimedia Commons har media som rör Vinkelhastighet.
  Bilder & media