Thomaes funktion

Thomaes function, Riemannfunktionen eller i engelsktalande länder popcornfunktionen är en funktion som är kontinuerlig i alla irrationella punkter och diskontinuerlig i alla rationella.

Thomaes funktion på intervallet $(0,1)$

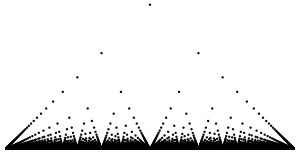
Funktionen definition är

$f(x)={\begin{cases}{\frac {1}{q}}&{\text{om }}x={\frac {p}{q}}\\0&{\text{i annat fall}}.\end{cases}}$, där $p$ och $q$ är heltal och bråket $p/q$ är förkortat så mycket som möjligt.

Kontinuitet i irrationella punkter

Låt $x$ vara ett irrationellt tal och $\epsilon =1/n\,$ för $n\,$ ett heltal. Vi kan definiera

$y^{*}=\min _{j}\min _{1\leq m\leq n}\left|x-{\frac {j}{m}}\right|$.

$y^{*}$ är alltså det kortaste avståndet till ett rationellt tal med nämnare högst $n$. Då är

$|f(x)-f(y)|=|f(y)|\leq \epsilon$ om $|x-y|\leq |x-y^{*}|=\delta$.

Detta visar att $f$ är kontinuerlig i $x$.

Diskontinuitet i rationella punkter

Om $x=p/q$ finns det för varje $\delta >0$ ett (irrationellt) $y$ så att

$|x-y|\leq \delta$ men $|f(x)-f(y)|=|f(x)|={\frac {1}{q}}$.

Detta visar att $f$ är diskontinuerlig i $x$.

Se även

• Dirichlets funktion

Externa länkar

• Wikimedia Commons har media som rör Thomaes funktion.
  Bilder & media