Riemanns zetafunktion eller Euler–Riemanns zetafunktion är en av de viktigaste funktionerna inom den komplexa analysen . Den används bland annat inom fysik , sannolikhetsteori och statistik . Det finns även en koppling mellan funktionen och primtalen , se Riemannhypotesen .[ 1] Hilbertproblemen som Millennieproblemen och är fortfarande obevisad.
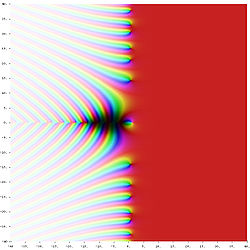
Riemanns zeta-funktion ζ (s ) i det komplexa planet. Färgen på en punkt s visar värdet av ζ (s): starka färger är för värden nära noll och nyansen visar värdet på argumentet. Den vita fläcken vid s = 1 är en pol , de svarta prickarna på den negativa reella axeln och på den kritiska linjen Re (er) = 1/2 är nollställen. Funktionen är den analytiska fortsättningen av serien
ζ
(
s
)
=
∑
n
=
1
∞
n
−
s
.
{\displaystyle \zeta (s)=\sum _{n=1}^{\infty }n^{-s}.}
Under 1700-talet undersökte Euler serien med reella värden på s :
∑
n
=
1
∞
n
−
s
=
1
1
s
+
1
2
s
+
1
3
s
+
.
.
.
{\displaystyle \sum _{n=1}^{\infty }n^{-s}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+...\!}
Serien konvergerar när s > 1.
Han upptäckte att serien ovan även kan uttryckas som en oändlig produkt över alla primtal .
Bernhard Riemann undersökte den i det komplexa talplanet och bevisade att funktionen konvergerar för hela komplexa talplanet då Re(s) > 1.[ 1]
Man kan definiera Riemanns zeta-funktion ζ(s) på två sätt, med hjälp av en Dirichletserie samt som en Eulerprodukt.
Riemanns zeta-funktion definieras för {s ∈ C: Re(s)>1}, d.v.s. s= σ + it, σ>1, enligt:
ζ
(
s
)
=
∑
n
=
1
∞
n
−
s
{\displaystyle \zeta (s)=\sum _{n=1}^{\infty }n^{-s}}
Enligt Cauchys intergraltest är denna serie konvergent inom det intervallet. Enligt Weierstrass kriterium är funktionen ζ(s) holomorfisk för Re(s)= σ >1 och därmed absolutkonvergent .
Euler visade år 1737[ 2]
∑
n
=
1
∞
1
n
s
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{s}}}}
kan skrivas om som en produkt över alla primtal:
∏
p
primtal
1
1
−
p
−
s
{\displaystyle \prod _{p{\text{ primtal}}}{\frac {1}{1-p^{-s}}}}
Man kan börja skriva om högerledet som en geometrisk serie :
∏
p
primtal
(
1
−
1
p
s
)
−
1
=
∏
p
primtal
(
1
+
1
p
s
+
1
p
2
s
+
…
)
=
∏
i
=
1
∑
n
i
=
0
∞
(
p
i
−
s
)
n
i
{\displaystyle \prod _{p{\text{ primtal}}}\left({1}-{\frac {1}{p^{s}}}\right)^{-1}=\prod _{p{\text{ primtal}}}\left(1+{\frac {1}{p^{s}}}+{\frac {1}{p^{2s}}}+\dots \right)=\prod _{i=1}\sum _{n_{i}=0}^{\infty }(p_{i}^{-s})^{n_{i}}}
där pi är det i :e primtalet.
I nästa steg utvecklar vi produkten av summan och vi får:
∏
i
=
1
∑
n
i
=
0
∞
(
p
i
−
s
)
n
i
=
∑
n
1
=
0
∞
(
p
1
−
s
)
n
1
.
∑
n
2
=
0
∞
(
p
2
−
s
)
n
2
⋯
=
∑
n
1
=
0
∞
∑
n
2
=
0
∞
…
(
p
1
n
1
p
2
n
2
…
)
−
s
{\displaystyle \prod _{i=1}\sum _{n_{i}=0}^{\infty }(p_{i}^{-s})^{n_{i}}=\sum _{n_{1}=0}^{\infty }(p_{1}^{-s})^{n_{1}}.\sum _{n_{2}=0}^{\infty }(p_{2}^{-s})^{n_{2}}\dots =\sum _{n_{1}=0}^{\infty }\sum _{n_{2}=0}^{\infty }\dots \left(p_{1}^{n_{1}}p_{2}^{n_{2}}\dots \right)^{-s}}
Nu kan vi med hjälp av aritmetikens fundamentalsats skriva om summorna: Eftersom varje primtalsuppdelning är unik, och alla tal kan skrivas som en produkt av primtal (och en oändlig mängd ettor), så kommer varje heltal att dyka upp en och endast en gång, och därmed kan vi skriva
∑
n
=
1
∞
1
n
s
=
∏
p
primtal
1
1
−
p
−
s
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p{\text{ primtal}}}{\frac {1}{1-p^{-s}}}}
För alla
C
{\displaystyle \mathbb {C} }
funktionalekvationen
ζ
(
1
−
s
)
=
2
(
2
π
)
s
cos
π
s
2
Γ
(
s
)
ζ
(
s
)
.
{\displaystyle \zeta (1-s)={2 \over (2\pi )^{s}}\ \cos {\frac {\pi s}{2}}\ \Gamma (s)\ \zeta (s).}
Den kan skrivas i den symmetriska formen
Γ
(
s
2
)
π
−
s
/
2
ζ
(
s
)
=
Γ
(
1
−
s
2
)
π
(
s
−
1
)
/
2
ζ
(
1
−
s
)
.
{\displaystyle \Gamma \left({\frac {s}{2}}\right)\ \pi ^{-s/2}\ \zeta (s)=\Gamma \left({\frac {1-s}{2}}\right)\ \pi ^{(s-1)/2}\ \zeta (1-s).}
Riemann definierade en annan funktion, Riemanns xi-funktion , med hjälp av vilken funktionalekvationen kan skrivas ännu kortare. Dess definition är
ξ
(
s
)
=
1
2
s
(
s
−
1
)
π
−
s
/
2
Γ
(
s
2
)
ζ
(
s
)
{\displaystyle \xi (s)={\frac {1}{2}}s(s-1)\ \pi ^{-s/2}\ \Gamma \left({\frac {s}{2}}\right)\ \zeta (s)}
och dess funktionalekvation är
ξ
(
s
)
=
ξ
(
1
−
s
)
.
{\displaystyle \!\ \xi (s)=\xi (1-s).}
Riemanns zeta-funktion är meromorfisk med en simpel pol för s = 1. Därför kan den utvecklas i en Laurentserie runt s = 1:
ζ
(
s
)
=
1
s
−
1
+
∑
n
=
0
∞
(
−
1
)
n
n
!
γ
n
(
s
−
1
)
n
.
{\displaystyle \zeta (s)={\frac {1}{s-1}}+\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n!}}\gamma _{n}\;(s-1)^{n}.}
Konstanterna γn Stieltjeskonstanterna och kan definieras som
γ
n
=
lim
m
→
∞
[
(
∑
k
=
1
m
(
log
k
)
n
k
)
−
(
log
m
)
n
+
1
n
+
1
]
.
{\displaystyle \gamma _{n}=\lim _{m\rightarrow \infty }{\left[\left(\sum _{k=1}^{m}{\frac {(\log k)^{n}}{k}}\right)-{\frac {(\log m)^{n+1}}{n+1}}\right]}.}
Konstanttermen γ0 är Eulers konstant .
En globalt konvergerande serie för zetafunktionen valid för alla komplexa tal s utom s = 1 + 2πin /log(2)n förmodades av Konrad Knopp och bevisades av Helmut Hasse 1930:
ζ
(
s
)
=
1
1
−
2
1
−
s
∑
n
=
0
∞
1
2
n
+
1
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
(
k
+
1
)
−
s
.
{\displaystyle \zeta (s)={\frac {1}{1-2^{1-s}}}\sum _{n=0}^{\infty }{\frac {1}{2^{n+1}}}\sum _{k=0}^{n}(-1)^{k}{n \choose k}(k+1)^{-s}.\!}
Hasse bevisade även serien
ζ
(
s
)
=
1
s
−
1
∑
n
=
0
∞
1
n
+
1
∑
k
=
0
n
(
n
k
)
(
−
1
)
k
(
k
+
1
)
s
−
1
.
{\displaystyle \zeta (s)={\frac {1}{s-1}}\sum _{n=0}^{\infty }{\frac {1}{n+1}}\sum _{k=0}^{n}{n \choose k}{\frac {(-1)^{k}}{(k+1)^{s-1}}}.}
En serie med Pochhammersymbolen är
ζ
(
s
)
=
s
s
−
1
−
∑
n
=
1
∞
(
ζ
(
s
+
n
)
−
1
)
s
(
s
+
1
)
⋯
(
s
+
n
−
1
)
(
n
+
1
)
!
.
{\displaystyle \zeta (s)={\frac {s}{s-1}}-\sum _{n=1}^{\infty }\left(\zeta (s+n)-1\right){\frac {s(s+1)\cdots (s+n-1)}{(n+1)!}}.\!}
För alla
s
∈
C
∖
{
1
}
{\displaystyle \scriptstyle s\in \mathbb {C} \setminus \{1\}}
ζ
(
s
)
=
2
s
−
1
s
−
1
−
2
s
∫
0
∞
sin
(
s
arctan
t
)
(
1
+
t
2
)
s
2
(
e
π
t
+
1
)
d
t
{\displaystyle \zeta (s)={\frac {2^{s-1}}{s-1}}-2^{s}\int \limits _{0}^{\infty }{\frac {\sin(s\arctan t)}{(1+t^{2})^{\frac {s}{2}}\ (\mathrm {e} ^{\pi \,t}+1)}}\,\mathrm {d} t}
och
ζ
(
s
)
=
1
s
−
1
+
1
2
+
2
∫
0
∞
sin
(
s
arctan
t
)
(
1
+
t
2
)
s
2
(
e
2
π
t
−
1
)
d
t
.
{\displaystyle \zeta (s)={\frac {1}{s-1}}+{\frac {1}{2}}+2\int \limits _{0}^{\infty }{\frac {\sin(s\arctan t)}{(1+t^{2})^{\frac {s}{2}}\ (\mathrm {e} ^{2\,\pi \,t}-1)}}\,\mathrm {d} t.}
För
R
e
s
>
1
{\displaystyle \scriptstyle \mathrm {Re} \,s>1}
ζ
(
s
)
=
1
s
−
1
+
1
2
+
∑
ν
=
2
q
B
ν
ν
!
∏
k
=
0
ν
−
2
(
s
+
k
)
−
1
q
!
∏
k
=
0
q
−
1
(
s
+
k
)
∫
1
∞
B
q
(
x
−
[
x
]
)
x
−
(
s
+
q
)
d
x
.
{\displaystyle \zeta (s)={\frac {1}{s-1}}\,+\,{\frac {1}{2}}\,+\,\sum \limits _{\nu =2}^{q}{\frac {\mathrm {B} _{\nu }}{\nu !}}\,\prod \limits _{k=0}^{\nu -2}(s+k)\,-\,{\frac {1}{q!}}\,\prod \limits _{k=0}^{q-1}(s+k)\,\int \limits _{1}^{\infty }\mathrm {B} _{q}(x-[x])\,x^{-(s+q)}\,\mathrm {d} x.}
En annan integral för
0
<
R
e
(
s
)
<
1
{\displaystyle 0<Re(s)<1\!}
∫
0
∞
x
s
−
1
γ
x
+
log
Γ
(
1
+
x
)
x
2
d
x
=
π
sin
(
π
s
)
ζ
(
2
−
s
)
2
−
s
{\displaystyle \int _{0}^{\infty }x^{s-1}{\frac {\gamma x+\log \Gamma (1+x)}{x^{2}}}\,dx={\frac {\pi }{\sin(\pi s)}}{\frac {\zeta (2-s)}{2-s}}\!}
Några specialfall för
s
=
1
2
{\displaystyle s={\frac {1}{2}}\!}
s
=
3
4
{\displaystyle s={\frac {3}{4}}\!}
∫
0
∞
γ
x
+
log
Γ
(
1
+
x
)
x
5
/
2
d
x
=
2
π
3
ζ
(
3
2
)
{\displaystyle \int _{0}^{\infty }{\frac {\gamma x+\log \Gamma (1+x)}{x^{5/2}}}\,dx={\frac {2\pi }{3}}\zeta \left({\frac {3}{2}}\right)}
∫
0
∞
γ
x
+
log
Γ
(
1
+
x
)
x
5
/
4
d
x
=
2
4
π
5
ζ
(
5
4
)
{\displaystyle \int _{0}^{\infty }{\frac {\gamma x+\log \Gamma (1+x)}{x^{5/4}}}\,dx={\sqrt {2}}{\frac {4\pi }{5}}\zeta \left({\frac {5}{4}}\right)}
En integral för zetafunktionens derivata är
ζ
′
(
s
)
=
2
s
−
1
(
log
2
s
−
1
−
1
(
s
−
1
)
2
+
∫
0
∞
2
arctan
t
⋅
cos
(
s
arctan
t
)
+
log
4
1
+
t
2
⋅
sin
(
s
arctan
t
)
(
1
+
t
2
)
s
2
⋅
(
e
π
t
+
1
)
d
t
)
{\displaystyle {\zeta '(s)=2^{s-1}\left({\frac {\log 2}{s-1}}-{\frac {1}{(s-1)^{2}}}+\int \limits _{0}^{\infty }{\frac {2\arctan t\cdot \cos(s\arctan t)+\log {\frac {4}{1+t^{2}}}\cdot \sin(s\arctan t)}{(1+t^{2})^{\frac {s}{2}}\cdot (e^{\pi t}+1)}}\mathrm {d} t\right)}}
som gäller för alla komplexa tal utom 1.
För alla
n
∈
N
∖
{
1
}
{\displaystyle \scriptstyle n\in \mathbb {N} \setminus \{1\}}
ζ
(
n
)
=
∫
0
1
⋯
∫
0
1
⏟
n
i
n
t
e
g
r
a
l
e
r
1
1
−
x
1
⋯
x
n
d
x
1
…
d
x
n
.
{\displaystyle \zeta (n)=\underbrace {\int \limits _{0}^{1}\dotsi \int \limits _{0}^{1}} _{n\mathrm {integraler} }{\frac {1}{1-x_{1}\dotsm x_{n}}}\,\mathrm {d} x_{1}\,\dotso \,\mathrm {d} x_{n}.}
Även om
ζ
(
1
)
=
∞
{\displaystyle \zeta (1)=\infty \!}
lim
s
→
1
(
s
−
1
)
ζ
(
s
)
=
1
,
{\displaystyle \lim _{s\to 1}(s-1)\zeta (s)=1,}
det vill säga zetafunktionen har en simpel pol vid s = 1 med residy 1.[ 1]
Zetafunktionen kan formellt ges som Mellintransformationen
2
π
−
s
/
2
Γ
(
s
/
2
)
ζ
(
s
)
=
∫
0
∞
θ
(
i
t
)
t
s
/
2
−
1
d
t
{\displaystyle 2\pi ^{-s/2}\Gamma (s/2)\zeta (s)=\int _{0}^{\infty }\theta (it)t^{s/2-1}\,dt}
med hjälp av Jacobis thetafunktion
θ
(
τ
)
=
∑
n
=
−
∞
∞
exp
(
π
i
n
2
τ
)
.
{\displaystyle \theta (\tau )=\sum _{n=-\infty }^{\infty }\exp(\pi in^{2}\tau ).}
Integralen konvergerar dock inte för något värde på s , men kan modifieras till följande uttryck för zetafunktionen:
π
−
s
/
2
Γ
(
s
/
2
)
ζ
(
s
)
=
1
s
−
1
−
1
s
+
1
2
∫
0
1
(
θ
(
i
t
)
−
t
−
1
/
2
)
t
s
/
2
−
1
d
t
+
1
2
∫
1
∞
(
θ
(
i
t
)
−
1
)
t
s
/
2
−
1
d
t
.
{\displaystyle {\begin{aligned}&{}\quad \pi ^{-s/2}\Gamma (s/2)\zeta (s)\\[6pt]&={\frac {1}{s-1}}-{\frac {1}{s}}+{\frac {1}{2}}\int _{0}^{1}\left(\theta (it)-t^{-1/2}\right)t^{s/2-1}\,dt+{\frac {1}{2}}\int _{1}^{\infty }(\theta (it)-1)t^{s/2-1}\,dt.\end{aligned}}}
Kopplingen mellan zetafunktionen och primtalen gör att zetafunktionen fortfarande är av intresse för matematiker. Riemannhypotesen som handlar om nollställen av zeta i sin tur som skulle kunna bestämma utbredning av alla primtal, en bättre approximation av de olika aritmetiska funktioner som t.ex. primtalfunktionen π(x).
Man kan hitta ett användningsområde av denna funktion även i statistik som ”Zipfs lag” och i matematiska teorier för stämning av musik. Inom fysik utnyttjas den i kaos i klassiska och kvantmekaniska system.
∑
k
=
2
∞
ζ
(
k
)
x
k
−
1
=
−
ψ
0
(
1
−
x
)
−
γ
{\displaystyle \sum _{k=2}^{\infty }\zeta (k)x^{k-1}=-\psi _{0}(1-x)-\gamma }
där ψ 0 är digammafunktionen .
∑
n
=
2
∞
(
ζ
(
n
)
−
1
)
=
1
{\displaystyle \sum _{n=2}^{\infty }(\zeta (n)-1)=1}
∑
n
=
1
∞
(
ζ
(
2
n
)
−
1
)
=
3
4
{\displaystyle \sum _{n=1}^{\infty }(\zeta (2n)-1)={\frac {3}{4}}}
∑
n
=
1
∞
(
ζ
(
2
n
+
1
)
−
1
)
=
1
4
{\displaystyle \sum _{n=1}^{\infty }(\zeta (2n+1)-1)={\frac {1}{4}}}
∑
n
=
2
∞
(
−
1
)
n
(
ζ
(
n
)
−
1
)
=
1
2
{\displaystyle \sum _{n=2}^{\infty }(-1)^{n}(\zeta (n)-1)={\frac {1}{2}}}
∑
n
=
1
∞
ζ
(
2
n
)
−
1
2
2
n
=
1
6
{\displaystyle \sum _{n=1}^{\infty }{\frac {\zeta (2n)-1}{2^{2n}}}={\frac {1}{6}}}
∑
n
=
1
∞
ζ
(
2
n
)
−
1
4
2
n
=
13
30
−
π
8
{\displaystyle \sum _{n=1}^{\infty }{\frac {\zeta (2n)-1}{4^{2n}}}={\frac {13}{30}}-{\frac {\pi }{8}}}
∑
n
=
1
∞
ζ
(
2
n
)
−
1
8
2
n
=
61
126
−
π
16
(
2
+
1
)
{\displaystyle \sum _{n=1}^{\infty }{\frac {\zeta (2n)-1}{8^{2n}}}={\frac {61}{126}}-{\frac {\pi }{16}}({\sqrt {2}}+1)}
∑
n
=
1
∞
(
ζ
(
4
n
)
−
1
)
=
7
8
−
π
4
(
e
2
π
+
1
e
2
π
−
1
)
{\displaystyle \sum _{n=1}^{\infty }(\zeta (4n)-1)={\frac {7}{8}}-{\frac {\pi }{4}}\left({\frac {e^{2\pi }+1}{e^{2\pi }-1}}\right)}
log
2
=
∑
n
=
1
∞
ζ
(
2
n
)
−
1
n
{\displaystyle \log 2=\sum _{n=1}^{\infty }{\frac {\zeta (2n)-1}{n}}}
log
π
=
∑
n
=
2
∞
(
2
(
3
2
)
n
−
3
)
(
ζ
(
n
)
−
1
)
n
.
{\displaystyle \log \pi =\sum _{n=2}^{\infty }{\frac {(2({\tfrac {3}{2}})^{n}-3)(\zeta (n)-1)}{n}}.}
Serier relaterade till Eulers konstant är
∑
n
=
2
∞
(
−
1
)
n
ζ
(
n
)
n
=
γ
{\displaystyle \sum _{n=2}^{\infty }(-1)^{n}{\frac {\zeta (n)}{n}}=\gamma }
∑
n
=
2
∞
ζ
(
n
)
−
1
n
=
1
−
γ
{\displaystyle \sum _{n=2}^{\infty }{\frac {\zeta (n)-1}{n}}=1-\gamma }
∑
n
=
2
∞
(
−
1
)
n
ζ
(
n
)
−
1
n
=
ln
2
+
γ
−
1
{\displaystyle \sum _{n=2}^{\infty }(-1)^{n}{\frac {\zeta (n)-1}{n}}=\ln 2+\gamma -1}
∑
n
=
2
∞
(
−
1
)
n
ζ
(
n
)
n
2
n
−
1
=
γ
−
log
4
π
{\displaystyle \sum _{n=2}^{\infty }(-1)^{n}{\frac {\zeta (n)}{n2^{n-1}}}=\gamma -\log {\frac {4}{\pi }}}
∑
n
=
1
∞
ζ
(
2
n
+
1
)
−
1
(
2
n
+
1
)
2
2
n
=
1
+
log
2
3
−
γ
.
{\displaystyle \sum _{n=1}^{\infty }{\frac {\zeta (2n+1)-1}{(2n+1)\ 2^{2n}}}=1+\log {\frac {2}{3}}-\gamma .}
En serie för Catalans konstant är
1
16
∑
n
=
1
∞
(
n
+
1
)
3
n
−
1
4
n
ζ
(
n
+
2
)
=
G
.
{\displaystyle {\frac {1}{16}}\sum _{n=1}^{\infty }(n+1)\ {\frac {3^{n}-1}{4^{n}}}\ \zeta (n+2)=G.}
∑
n
=
1
∞
(
−
1
)
n
t
2
n
[
ζ
(
2
n
)
−
1
]
=
t
2
1
+
t
2
+
1
−
π
t
2
−
π
t
e
2
π
t
−
1
{\displaystyle \sum _{n=1}^{\infty }(-1)^{n}t^{2n}\left[\zeta (2n)-1\right]={\frac {t^{2}}{1+t^{2}}}+{\frac {1-\pi t}{2}}-{\frac {\pi t}{e^{2\pi t}-1}}}
∑
k
=
0
∞
ζ
(
k
+
n
+
2
)
−
1
2
k
(
n
+
k
+
1
n
+
1
)
=
(
2
n
+
2
−
1
)
ζ
(
n
+
2
)
−
1
{\displaystyle \sum _{k=0}^{\infty }{\frac {\zeta (k+n+2)-1}{2^{k}}}{{n+k+1} \choose {n+1}}=\left(2^{n+2}-1\right)\zeta (n+2)-1}
∑
k
=
0
∞
(
k
+
ν
+
1
k
)
[
ζ
(
k
+
ν
+
2
)
−
1
]
=
ζ
(
ν
+
2
)
{\displaystyle \sum _{k=0}^{\infty }{k+\nu +1 \choose k}\left[\zeta (k+\nu +2)-1\right]=\zeta (\nu +2)}
∑
k
=
0
∞
(
k
+
ν
+
1
k
+
1
)
[
ζ
(
k
+
ν
+
2
)
−
1
]
=
1
{\displaystyle \sum _{k=0}^{\infty }{k+\nu +1 \choose k+1}\left[\zeta (k+\nu +2)-1\right]=1}
∑
k
=
0
∞
(
−
1
)
k
(
k
+
ν
+
1
k
+
1
)
[
ζ
(
k
+
ν
+
2
)
−
1
]
=
2
−
(
ν
+
1
)
{\displaystyle \sum _{k=0}^{\infty }(-1)^{k}{k+\nu +1 \choose k+1}\left[\zeta (k+\nu +2)-1\right]=2^{-(\nu +1)}}
∑
k
=
0
∞
(
−
1
)
k
(
k
+
ν
+
1
k
+
2
)
[
ζ
(
k
+
ν
+
2
)
−
1
]
=
ν
[
ζ
(
ν
+
1
)
−
1
]
−
2
−
ν
{\displaystyle \sum _{k=0}^{\infty }(-1)^{k}{k+\nu +1 \choose k+2}\left[\zeta (k+\nu +2)-1\right]=\nu \left[\zeta (\nu +1)-1\right]-2^{-\nu }}
∑
k
=
0
∞
(
−
1
)
k
(
k
+
ν
+
1
k
)
[
ζ
(
k
+
ν
+
2
)
−
1
]
=
ζ
(
ν
+
2
)
−
1
−
2
−
(
ν
+
2
)
{\displaystyle \sum _{k=0}^{\infty }(-1)^{k}{k+\nu +1 \choose k}\left[\zeta (k+\nu +2)-1\right]=\zeta (\nu +2)-1-2^{-(\nu +2)}}
Några serier av Adamchik och Srivastava:
∑
n
=
1
∞
t
2
n
n
ζ
(
2
n
)
=
log
(
π
t
sin
(
π
t
)
)
{\displaystyle \sum _{n=1}^{\infty }{\frac {t^{2n}}{n}}\zeta (2n)=\log \left({\frac {\pi t}{\sin(\pi t)}}\right)}
∑
n
=
2
∞
n
m
[
ζ
(
n
)
−
1
]
=
1
+
∑
k
=
1
m
k
!
S
(
m
+
1
,
k
+
1
)
ζ
(
k
+
1
)
{\displaystyle \sum _{n=2}^{\infty }n^{m}\left[\zeta (n)-1\right]=1\,+\sum _{k=1}^{m}k!\;S(m+1,k+1)\zeta (k+1)}
och
∑
n
=
2
∞
(
−
1
)
n
n
m
[
ζ
(
n
)
−
1
]
=
−
1
+
1
−
2
m
+
1
m
+
1
B
m
+
1
−
∑
k
=
1
m
(
−
1
)
k
k
!
S
(
m
+
1
,
k
+
1
)
ζ
(
k
+
1
)
{\displaystyle \sum _{n=2}^{\infty }(-1)^{n}n^{m}\left[\zeta (n)-1\right]=-1\,+\,{\frac {1-2^{m+1}}{m+1}}B_{m+1}\,-\sum _{k=1}^{m}(-1)^{k}k!\;S(m+1,k+1)\zeta (k+1)}
där
B
k
{\displaystyle B_{k}}
Bernoullitalen och
S
(
m
,
k
)
{\displaystyle S(m,k)}
Stirlingtalen av andra ordningen .
Man kan uttrycka det inverterade värdet av zeta-funktionen med hjälp av Möbiusfunktionen μ(n ) på följande sätt:
1
ζ
(
s
)
=
∑
n
=
1
∞
μ
(
n
)
n
s
{\displaystyle {\frac {1}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}}
för varje komplext tal s med realdel > 1.
A A Karatsuba, S M Voronin (mathematician) (1992-12-01). The Riemann Zeta-Function ISBN 9783110131703 S J Patterson (1995-02-01). An Introduction to the Theory of the Riemann Zeta-Function ISBN 9780521499057 Roman J. Dwilewicz, Ján Mináč. ”Values of the Riemann zeta function at integers” . http://www.mat.uab.cat/matmat/PDFv2009/v2009n06.pdf . Läst 5 september 2012 . Sondow, Jonathan; Weisstein, Eric W.. ”Riemann Zeta Function” . Wolfram Research. https://mathworld.wolfram.com/RiemannZetaFunction.html . Läst 5 september 2012 . Apostol, T. M. (2010), ”Zeta and Related Functions” , i Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F. m.fl., NIST Handbook of Mathematical Functions MR 2723248 ISBN 978-0521192255 Jonathan Borwein , David M. Bradley, Richard Crandall (2000). ”Computational Strategies for the Riemann Zeta Function” (PDF). J. Comp. App. Math. 121 (1–2): sid. 247–296. doi :10.1016/S0377-0427(00)00336-8 . http://www.maths.ex.ac.uk/~mwatkins/zeta/borwein1.pdf . Cvijović, Djurdje; Klinowski, Jacek (2002). ”Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments”. J. Comp. App. Math. 142 (2): sid. 435–439. doi :10.1016/S0377-0427(02)00358-8 Cvijović, Djurdje; Klinowski, Jacek (1997). ”Continued-fraction expansions for the Riemann zeta function and polylogarithms”. Proc. Amer. Math. Soc. 125 (9): sid. 2543–2550. doi :10.1090/S0002-9939-97-04102-6 H. M. Edwards (1974). Riemann's Zeta Function ISBN 0-486-41740-9 Hadamard, Jacques (1896). ”Sur la distribution des zéros de la fonction ζ (s ) et ses conséquences arithmétiques”. Bulletin de la Societé Mathématique de France 14: sid. 199–220. G. H. Hardy (1949). Divergent Series Hasse, Helmut (1930). ”Ein Summierungsverfahren für die Riemannsche ζ -Reihe”. Math. Z. 32: sid. 458–464. doi :10.1007/BF01194645 A. Ivic (1985). The Riemann Zeta Function ISBN 0-471-80634-X Y. Motohashi (1997). Spectral Theory of the Riemann Zeta-Function ISBN 0521445205 A. A. Karatsuba; S.M. Voronin (1992). The Riemann Zeta-Function Mező, István; Dil, Ayhan (2010). ”Hyperharmonic series involving Hurwitz zeta function”. Journal of Number Theory 130 (2): sid. 360–369. doi :10.1016/j.jnt.2009.08.005 Donald J. Newman (1998). Analytic number theory GTM . "177". Springer-Verlag. ISBN 0-387-98308-2 Raoh, Guo (1996). ”The Distribution of the Logarithmic Derivative of the Riemann Zeta Function”. Proceedings of the London Mathematical Society s3–72: sid. 1–27. doi :10.1112/plms/s3-72.1.1 Riemann, Bernhard (1859). ”Über die Anzahl der Primzahlen unter einer gegebenen Grösse” . Monatsberichte der Berliner Akademie . http://www.maths.tcd.ie/pub/HistMath/People/Riemann/Zeta/ . Gesammelte Werke , Teubner, Leipzig (1892), Återutgiven av Dover, New York (1953).Sondow, Jonathan (1994). ”Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series”. Proc. Amer. Math. Soc. 120 (120): sid. 421–424. doi :10.1090/S0002-9939-1994-1172954-7 E.C. Titchmarsh (1986). The Theory of the Riemann Zeta Function, Second revised (Heath-Brown ) edition E.T. Whittaker och G.N. Watson (1927). A Course in Modern Analysis , fourth edition, Cambridge University Press (Chapter XIII).Zhao, Jianqiang (1999). ”Analytic continuation of multiple zeta functions”. Proc. Amer. Math. Soc. 128 (5): sid. 1275–1283. doi :10.1090/S0002-9939-99-05398-8 Linus Bergkvist. ”Nollställena till Riemanns Zeta-funktion och dess beteende på den kritiska linjen” . Arkiverad från originalet den 2 februari 2017. https://web.archive.org/web/20170202092909/http://www.math.su.se/polopoly_fs/1.141051.1373274078!/menu/standard/file/Nollstallen_Riemanns_Zetafunktion.pdf .