Dickmans funktion
Inom analytisk talteori är Dickmans funktion eller Dickman–de Bruijns funktion ρ en speciell funktion som används till att uppskatta antalet släta tal mindre än en given storhet. Den introducerades av Karl Dickman i hans enda matematiska publikation och studerades vidare av Nicolaas Govert de Bruijn.[1][2][3]
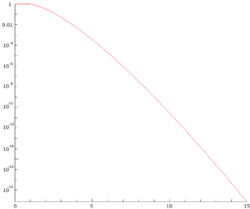
Definition
redigeraDickman-de Bruijns funktion är en kontinuerlig funktion som satisfierar differentialekvationen
med villkoret för 0 ≤ u ≤ 1. Dickman bevisade att då är fixerat är
där är antalet y-glatta tal inte större än x.
V. Ramaswami bevisade senare att är asymptotiskt lika med med felterm
Referenser
redigera- Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Dickman function, 5 februari 2014.
Noter
redigera- ^ Dickman, K. (1930). ”On the frequency of numbers containing prime factors of a certain relative magnitude”. Arkiv för Matematik, Astronomi och Fysik 22A (10): sid. 1–14.
- ^ de Bruijn, N. G. (1951). ”On the number of positive integers ≤ x and free of prime factors > y”. Indagationes Mathematicae 13: sid. 50–60. http://alexandria.tue.nl/repository/freearticles/597499.pdf.
- ^ de Bruijn, N. G. (1966). ”On the number of positive integers ≤ x and free of prime factors > y, II”. Indagationes Mathematicae 28: sid. 239–247. http://alexandria.tue.nl/repository/freearticles/597534.pdf.
- ^ Ramaswami, V. (1949). ”On the number of positive integers less than and free of prime divisors greater than xc”. Bulletin of the American Mathematical Society 55: sid. 1122–1127. http://www.ams.org/bull/1949-55-12/S0002-9904-1949-09337-0/S0002-9904-1949-09337-0.pdf.
Externa länkar
redigera- Broadhurst, David (2010). ”Dickman polylogarithms and their constants”. https://arxiv.org/abs/1004.0519.
- Soundararajan, K. (2010). ”An asymptotic expansion related to the Dickman function”. https://arxiv.org/abs/1005.3494.
- Weisstein, Eric W., "Dickman function", MathWorld. (engelska)