Inom matematiken är de hyperboliska funktionerna nära besläktade med de trigonometriska funktionerna, vilket antyds av deras benämningar:
- sinus hyperbolicus (sinh)
- cosinus hyperbolicus (cosh)
- tangens hyperbolicus (tanh)
- secans hyperbolicus (sech)
- cosecans hyperbolicus (csch)
- cotangens hyperbolicus (coth)

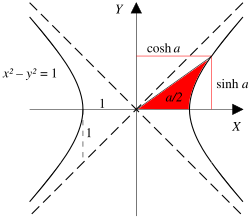
sech och csch används sällan.
Definition
redigeraDe hyperboliska funktionernas definitioner är
Vid jämförelse med Eulers formler, framgår att enligt definitionerna av cosh och cos är skillnaden att vinkeln är multiplicerad med komplexa enheten i; motsvarande gäller för sin och sinh:
och därmed kan de trigonometriska funktionerna – ur ett analytiskt perspektiv – betraktas som utvidgningar av de hyperboliska funktionerna till det komplexa talplanet. Ur ett geometriskt perspektiv är dock de trigonometriska funktionerna mer grundläggande och man kan då – ur denna synvinkel – betrakta de hyperboliska funktionerna som utvidgningar till det komplexa talplanet av trigonometriska funktioner.
Taylorserie
redigeraUtveckling av sinh och cosh i en taylorserie kan göras med hjälp av serieutvecklingar av exponentialfunktionen:
Identiteter
redigeraMotsvarigheten till trigonometriska ettan, kallad hyperboliska ettan:
Summor:
Inversa funktioner
redigeraDe hyperboliska funktionernas inverser benämns area hyperbolicus eller arcus hyperbolicus. Dock kan varje sådan invers-funktion skrivas med hjälp av logaritmer:
Speciellt gäller att arcsinh är entydigt definierad för hela ℝ till skillnad från inverserna av de trigonometriska funktionerna där man undviker flertydighet genom att införa begreppet principalvärde.
Derivator
redigeraSe även
redigeraExterna länkar
redigera- Wikimedia Commons har media som rör Hyperbolisk funktion.
- GonioLab: Visualisering av enhetscirkeln, trigonometriska och hyperboliska funktioner (Java Web Start)