Fil:Pi 30K.gif
Pi_30K.gif (500 × 500 pixlar, filstorlek: 476 kbyte, MIME-typ: image/gif, upprepad, 10 bildrutor, 2,0 s)
Filhistorik
Klicka på ett datum/klockslag för att se filen som den såg ut då.
| Datum/Tid | Miniatyrbild | Dimensioner | Användare | Kommentar | |
|---|---|---|---|---|---|
| nuvarande | 16 februari 2017 kl. 17.00 | 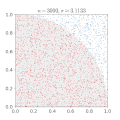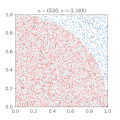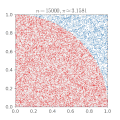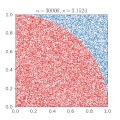 | 500 × 500 (476 kbyte) | Nicoguaro | Make the plot square and increase gif delay. |
| 16 februari 2017 kl. 16.38 |  | 640 × 480 (476 kbyte) | Nicoguaro | Bigger text in the axes, and colors from ColorBrewer. Code in Python. | |
| 7 november 2011 kl. 19.29 | 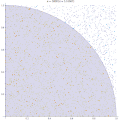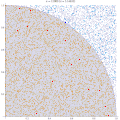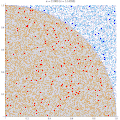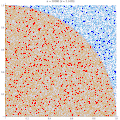 | 500 × 500 (373 kbyte) | Rayhem | Slowed animation to avoid looking like a blinky page element, improved resolution, added counter for number of points, shaded points inside/outside the circle. ==Mathematica 7.0 Source== <pre> tinyColor[color_, point_] := {PointSize[Small], color, Point[ | |
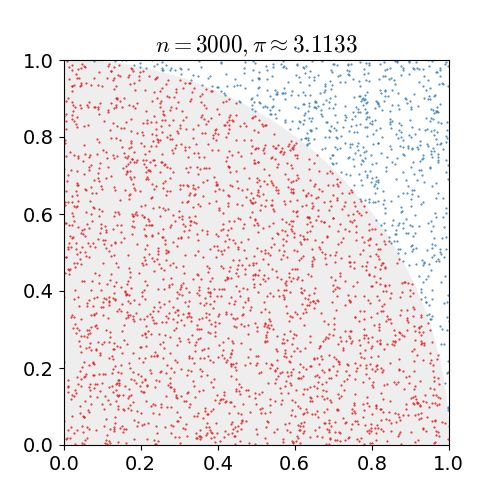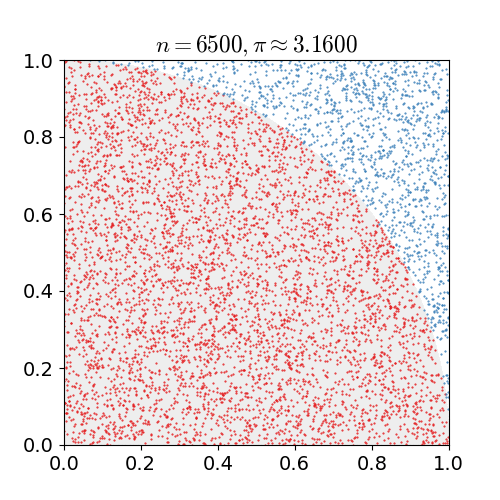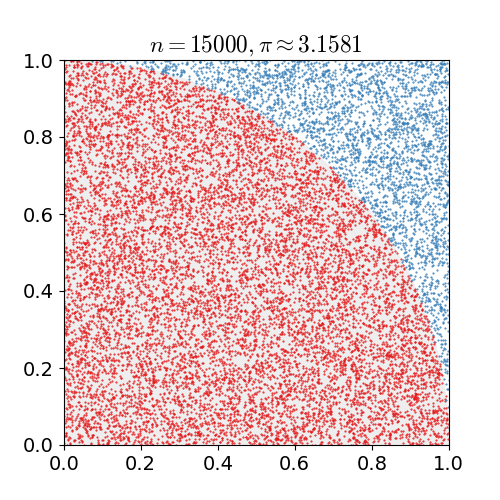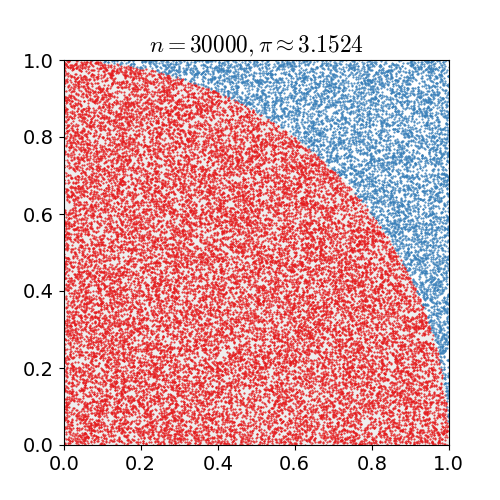
| 15 mars 2011 kl. 00.12 |  | 360 × 369 (363 kbyte) | CaitlinJo | {{Information |Description ={{en|1=As points are randomly scattered inside the unit square, some fall within the unit circle. The fraction of points inside the circle over all points approaches pi as the number of points goes toward infinity. This ani |
Filanvändning
Följande sida använder den här filen:
Global filanvändning
Följande andra wikier använder denna fil:
- Användande på ar.wiki.x.io
- Användande på be.wiki.x.io
- Användande på bg.wiki.x.io
- Användande på ca.wiki.x.io
- Användande på da.wiki.x.io
- Användande på el.wiki.x.io
- Användande på en.wiki.x.io
- Användande på en.wikibooks.org
- Användande på eo.wiki.x.io
- Användande på eu.wiki.x.io
- Användande på fa.wiki.x.io
- Användande på fr.wiki.x.io
- Användande på he.wiki.x.io
- Användande på hi.wiki.x.io
- Användande på id.wiki.x.io
- Användande på it.wiki.x.io
- Användande på ja.wiki.x.io
- Användande på ko.wiki.x.io
- Användande på pt.wiki.x.io
- Användande på sh.wiki.x.io
- Användande på simple.wiki.x.io
- Användande på sl.wiki.x.io
- Användande på sr.wiki.x.io
- Användande på ta.wiki.x.io
- Användande på test.wiki.x.io
- Användande på th.wiki.x.io
- Användande på tr.wiki.x.io
- Användande på uk.wiki.x.io
- Användande på vi.wiki.x.io
- Användande på www.wikidata.org
- Användande på zh-yue.wiki.x.io
- Användande på zh.wiki.x.io