En enhetscirkel är en cirkel i planet med radie 1. Ofta talar man om enhetscirkeln och avser då en enhetscirkel med mittpunkt i origo.
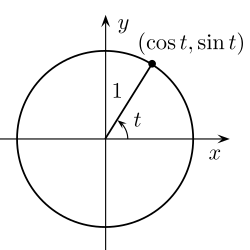
Av Pythagoras sats följer att enhetscirkeln kan beskrivas i kartesiska koordinater som mängden av punkter (x, y) sådana att x2 + y2 = 1. I polära koordinater blir detta den trigonometriska ettan.[1]
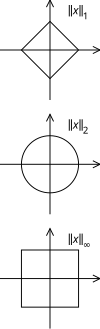
Mer allmänt används enhetscirklar med avseende på olika normer, då en enhetscirkel består av de punkter vars norm är lika med 1.
Omkrets och area
redigeraEnhetscirkelns omkrets erhålls genom att sätta radien, r, till 1 i formeln för en cirkels omkrets[2] enligt:
Arean för området som avgränsas av en enhetscirkel erhålls på motsvarande sätt med formeln för en cirkelskivas area:[3]
Koordinatberäkning
redigeraFör att beräkna de kartesiska koordinaterna (x, y) för en punkt på enhetscirkeln som befinner sig vid vinkeln t mätt från x-axeln kan man använda cosinus och sinus:[4]
Se även
redigeraReferenser
redigera- ^ Thompson, Jan; Thomas Martinsson (1991). Wahlström & Widstrands matematiklexikon. Wahlström & Widstrand. sid. 104. ISBN 91-46-16515-0
- ^ ”Circumference (Perimeter) of a circle”. https://www.mathopenref.com/circumference.html. Läst 29 november 2020.
- ^ ”Area enclosed by a circle”. https://www.mathopenref.com/circlearea.html. Läst 29 november 2020.
- ^ ”Unit Circle”. https://www.mathopenref.com/unit-circle.html. Läst 29 november 2020.
Externa länkar
redigera- Wikimedia Commons har media som rör Enhetscirkel.
- GonioLab: Visualisering av enhetscirkeln, trigonometriska och hyperboliska funktioner (Java Web Start)